My First Experimental Result
This is a narrative of how I figured something out about string tension and the main resonances of a mandolin body. Bear with me…
At first, I only tapped the tops.
That gave me FFT graphs with either one or two main peaks. I wondered why only one or two? They look like this, left to right: 1 main peak, kind of 2 main peaks, and definitely 2 main peaks. Where are these frequencies coming from?
One would assume that since one is tapping the top the loudest frequency should be coming from the top. But one assumes incorrectly.
...quick side-bar ...
My journal is fuzzy at this point, but the next entry suggests I learned that the first highest peak is the main air resonance, often called A0 (as I will here). This is the flexible resonator version of a Helmholtz resonator. I will not go into it too deeply.* The Helmholtz resonance is the note you get when you blow over a bottle. For Helmholtz's work and resonance equation, the frequency of his resonators will depend on 1) the volume of air in the cavity, 2) the area of the opening, and 3) the length of the neck. Since wooden instruments have less rigid sides with resonances of their own, and there is no real “neck”, we can’t use Helmholtz’s equation exactly, but we can work with the essence of the idea. For this reason the actual Helmholtz frequency of an instrument is not the same as the main air, A0, and we will spend our time with A0 since it is the one doing work here… and there’s more to say here.. and I've written more than I meant...
… side-bar over… Onward!
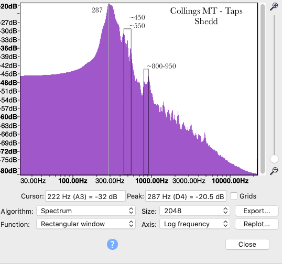
To drive this point home, here is another mandolin with the taps on the left and blowing over the soundhole on the right. The first two main peaks have the same frequencies— the first one is the A0 at 305 Hz.
So I got curious because if the first peak has mostly to do with air, and sometimes there is only one main peak... what is that second one? The top?
Yep! The second main peak is the top if you are hitting the top. Onward!
So I thought, why doesn't the back show up in the top taps? Surely it resonates when the instrument resonates. So, I tapped the back as well as the top and here's how that graph looks (this is from a different mandolin so the numbers are different, but the idea is the same)...
OK! Three prominent peaks (293, 422 and 507— the A0, main top and main back)! This third main peak showed up when I tapped the back so it must be the main back frequency. Onward!
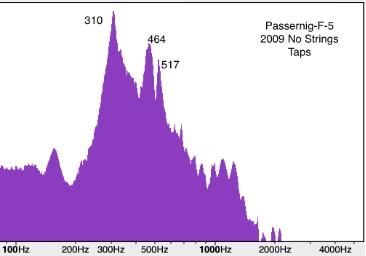
From Gore/Gilet and other sources I thought it may be worth doing these taps graphs without strings on. After all, you don't get to put strings on until it's all put together**, and that could be too late to make some adjustments. I wondered if the resonant peaks would stay the same with the strings off? Here’s the same mandolin from the last graph tapped top and back with no strings on it.
There are still three prominent peaks, but they aren't quite spaced the same. Notice how the main peaks moved up: the A0 293 --> 310 , main top 422 --> 464 and main back 507 --> 517! Why??? Is removing strings like removing mass (remember adding mass causes frequencies to drop, so removing mass causes them to raise)? And... Why does the back change when nothing was done to it?
I mulled over this for a while before figuring a way to figure it out. I decided to take another instrument and did taps at full string tension, then tuned down to an octave below full tension (we will just call it "half tension"), then at just enough tension to keep the bridge in place ("min tension) and then with no tension and no bridge. Those graphs look like this. I switched to Xcel for this graph, apologize about no scale for the x-axis, this is 0-900 Hz logarithmic....
I must have stared at this for several hours before it struck me. See how the gray (full tension), blue (half tension), and orange (min tension) peaks all stack up with each other for the peaks at the A0, the main top and main back areas, but the yellow peak is to the right in each case? That's because the yellow line is the only one where the bridge is not attached to the top! No matter the tension on the strings, the three main resonances stay the same--but removing the bridge makes things change! This is a mass issue, not a tension issue!
It's the bridge dummy! Ha!
This discovery felt magical because it was the first time I experimentally answered one of my own questions. In further testing I've learned there is a range of change for each of the resonances with the bridge on or off. Not only did I identify the cause, I've been able to quantify its impact. This got me hooked!
… one more side-bar…
I will point out in that attaching the bridge to the back of the instrument (poster putty and sturdy tape) caused the A0 to drop the same amount as if it is taped to the top. Fascinating result but that's all I have to say about it for now...
… side-bar over… Onward!
So what does that mean for tone? oh ho ho ho ho ... no not yet. We don't know anything about tone yet, but we do know one way in which these resonances interact with each other! And, from a building perspective, we now have a clue about mass and the three main resonances: the A0, main top and main back.
And now we have good reason to care about bridge mass, and also mass in the top and back plates. But I will end it here with the promise to share about a bridge mass experiment I’ve done in light on this, but at another time!
*I highly encourage you to look up more about Hermann Von Helmholtz!
**I am working on something to negate this statement